コンピューターのデータと各用語 　ちょっと大変ですが、コンピューターそのものの話と、用語について。 　コンピューターのデータはすべて０と１で表されます。これはオセロのコマの裏表のようなものだと考えてください。データを蓄える場所＝メモリには、この「オセロのコマ」がいっぱい並んでいて、それぞれが「裏」や「表」になっていて、データが格納されているというようなイメージを浮かべると、分かりやすいと思います。 　このコマひとつを「ビット」という単位で表します。コマの裏表を１と０で表すと、１ビットはこの２種類の状態を持つことになります。 　これを並べて、例えば「００１１」であれば、４桁なので４ビットになります。一桁増えるごとに倍のデータを格納できるようになり、全体では「２の桁数乗」のデータを格納できます。実際にオセロのコマを並べてみて、何通りの組み合わせがあるか、確かめてみてください。４ビットなら４桁なので、２の４乗＝１６通りの組み合わせができるはずです。これだけの数、データを格納できるということです。 　またＶＣ５．０等で使われる型でよく「３２ビット値」というものが出てきますが、これはこの１と０（つまりビット）が３２桁並んでひとまとめという意味です。このように、ビットとはどれだけの数のデータを格納できるかということを表す単位なのです。 　ビットは「２進数」です。つまり「２になったら一桁繰り上がり、元の桁は０になる」ということです。普通日常生活で使う「１０進数」は、１０になったらひとつ繰り上がります。これと比べてみてください。例えば「０１０１」に１を足せば、一番右の位が「１＋１＝２」になって「繰り上がり＋０」になり、「０１１０」という結果になります。 　ビットはあまりにも単位が小さいので、普段は使用しません。普段は次のふたつの量を使って計算します。 　ひとつは「１６進数」です。１６進数はその名の通り「１６になったら一桁繰り上がる数」です。１から９までは１０進数と同じですが、１０から１５をＡからＦで表します。ホームページの色指定に使うので、結構なにげに使ってる人もいるでしょう。 　１６進数は一桁で４ビットの値を格納できます。それだけ、大きな値を表すことができるというわけです。 　Ｃ言語では「普通の１０進数じゃなくて１６進数ですよー」と示す場合には「０ｘ」を付けます。例えば「０ｘ５ｂ」みたいな感じです。ちなみにアルファベットは大文字でも小文字でもＯＫ。あと当然プログラミングでは半角英数でね。 　この「ビット−１６進」変換はめんどいですが、実は簡単にできます。アクセサリの「電卓」を実行して、「電卓の種類」を「関数電卓」にしてください。電卓が大きくなりましたね。左上のボタンが「１０進」になっているのを確認して数字を入力。そのあと左隣の「１６進」にすればあーら簡単、１０進数が１６進数に変換されちゃいました。簡単ですねー。逆ももちろんＯＫ（アルファベットは数字キーの下のＡ〜Ｆを使って入力してください）。とりあえず「テストに出る」とかじゃないのなら、これを使うのが一番手っ取り早いでしょう。 　さて、もうひとつの量は「バイト」です。バイトは１６進数で２桁、つまり８ビットを表します。１０進数だと「２の８乗＝２５６」種類のデータを格納できるということになります。 　Ｃ言語のすべてのデータ型はこのバイト単位で計算します。最小単位のchar型は１バイトですし、malloc()等で取得するバッファサイズも、バイト単位で指定しますし、sizeof()で返ってくる変数のサイズも、バイト単位です。 　基本的に、プログラミングで使うのはこのみっつ、「ビット」「バイト」「１６進数」です。

整数の中身 　さて問題です。−１と４２９４９６７２９５は等しい？　ま、結果は次のコードを試してみれば一目瞭然でしょう。

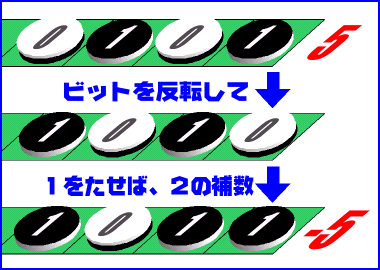
マイナスと「２の補数」 　１６進数で「マイナス」を表すときには、一番上のビットを１にするだけではできません。その証拠に、−１はＦＦＦＦＦＦＦＦです。この特殊なマイナスの数字は「２の補数」という方法を使って求めます。 　「２の補数」の言葉の意味は考えなくていいです。単に方法だけ憶えておけばいいでしょう。 　方法は簡単。「ビットを反転し、１を足す」だけ。例えば「０１０１」（５）なら、ビットを反転して「１０１０」、これに１を足して「１０１１」。これが「−５」を表します。簡単ですねー。ビット数は違いますが、「０００１」なら「１１１１」、つまり０ｘＦとなります。これで−１がＦＦＦＦＦＦＦＦになる理由が分かりましたね。 　なんでまたこんなめんどくさいことをするのかというと、２の補数を使うと「足し算で引き算ができる」からです。んなバカな、と思うかもしれませんがちゃんとできてしまうのです。 　例として「７−４＝３」を計算してみましょう。７は「０１１１」、４は「０１００」になります。ここで４の「２の補数」は「１１００」となり、これが「−４」を表します。この時点で、式は「７＋（−４）」となります。これを計算すると「１００１１」、一番上の１を無視して「００１１」、つまり３になったというわけです。 　なんでまたこんなことをするのかというと、理由はふたつあります。ひとつは「引き算をしなくていい」ということ。足し算とビット反転さえできればコンピューターの中にわざわざ「引き算の回路」を作らなくて済むというわけです。もうひとつは「繰り下がりを気にしなくていい」という部分があります。繰り下がりは繰り上がりに比べて面倒なので、しない方が楽に済みます。 　まぁ、「こういうことができるから２の補数をマイナスにしよう」ということでもあるし、この辺はむかーしのコンピューターの名残だったりするので、「マイナスは２の補数でできてるんだ」ってことを感じていればいいでしょう。単にマイナスの値を求めるのであれば、実際にこの方法を使わずに、さっき書いた「計算機」を使えば簡単に出せますし。 　ちなみに「なんで足し算で引き算ができるんだよーっ！！」という人のために、簡単な例で種明かしをしましょう。 　実は、「２の補数を作る」ということは、１０進数なら「１０の桁数乗から引く」ことをなのです。たとえば「３」は「１０−３＝４」が、「５７」なら「１００−５７＝４３」が、それぞれの２の補数になるというわけです。 　同じく２進数の場合、「０１」なら「１００−０１＝１１」、「０１０１」なら「１００００−０１０１＝１０１１」が２の補数になります。でも「一桁多い数字」を作るのはめんどくさいので、「１００００＝１１１１＋１」のようにふたつに分けます。さらに「１１１１」から２進数を引くと、必ず「引いたものの反転」という結果になります。この結果から、２進数の場合「反転して１を足す」ことが、「１０の桁数乗から引く」ことと一致することが分かります。 （この辺の解説が間違っていたので訂正しました） 　さて次に、確認のために「１０進数」で２の補数を使った引き算を実行してみましょう。同じく例は「７−４」にします。 　４の「２の補数」をまず作ってみましょう。この場合「４」は一桁ですから、１０進数では「１０×１から引く」ことで求まりますので、「１０−４＝６」が「４の２の補数」ということになります。 　この変換で、式は「７＋６＝１３」、上の位を消して「３」、見事に答が出たということです。 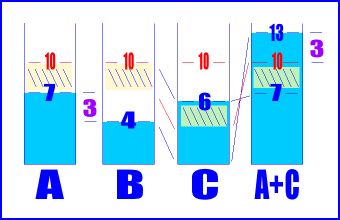　これを、簡単な例と図を使って説明しましょう。 　「１０」の目盛りが書かれたビーカーがふたつあったとします。Ａには「７」まで水が、Ｂには「４」まで水が入っているとします。さて、水の量の差はいくらでしょうか。 　これは単に、水位の差を調べれば簡単に分かりますね。水の高さの差は３、つまり答は３ってことになります。 　さて、では足し算を使ってこの差を求めてみましょう。まずなんらかの方法を使って「Ｂの水位から１０の目盛りまで」と同じ量の水を用意します。これが「２の補数の作製」にあたります。 　この「Ｂの水位から１０の目盛りまで」と同じ量の水（Ｃとします）をＡに入れます。１０の目盛りを超えることになるでしょう。で、実はこの「１０の目盛りから水位まで」が、答、つまり「水位の差」と一致するのです。これで、足し算で引き算ができてしまったことになります。 　なぜこの差が足し算で求まってしまうのでしょう。もういちどＢのビーカーを見てください。Ｃの水を作った領域はふたつに分けられます。ひとつは「１０の目盛りからＡの水位」までの領域、もうひとつは「Ａの水位からＢの水位（つまりこれが答）」までの領域です。 　ＣをＢに入れた時、「１０の目盛りからＡの水位」までの領域の水は、当然Ａの方も空なので、そのまますっぽり入ってしまうことになります。ということは、これだけでＡは１０の目盛りまで満たされることになります。で、そこに「Ａの水位からＢの水位」＝答が入ります。この水の水位は１０の目盛りからなので、これを計れば答が出てくるというわけです。 　これと同じことを２進数でも行うことで、足し算と２の補数を使って引き算ができてしまうのです。ただその中で、「反転して１を足す」というテクニックを用いている部分がちょっと違うくらいです。 　なーんか腑に落ちないかもしれません。現実的にはＣの水を作ること自体が難しいんですが、コンピューターの世界では「ビット反転」は簡単にできてしまうので、この方法が採られるというわけです。

つづく 　ちょっと長くなっちゃたので、次回に続きます。