補数
| 日本語 | 補う数 |
| 英語 | complement |
| ふりがな | ほすう |
| フリガナ | ホスウ |
各桁において「繰り上がる数」から引いた数。
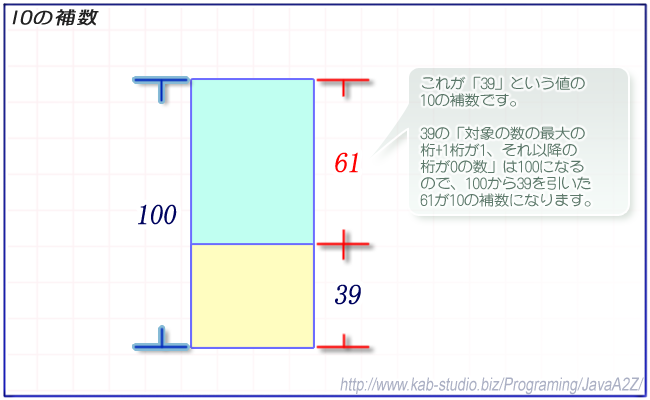
ある数の「逆の数」「補う数」のこと。たとえば10進数の場合「3」の補数は「7」であり、「39」の補数は「61」である。
正確には、補数には「Nの補数」と「N-1の補数」の2種類がある。
「N」には、対象の数の進数が入る。10進数であれば「10の補数」と「9の補数」があり、2進数であれば「2の補数」と「1の補数」がある。
そのため、たとえば10進数において「8の補数」等は存在しないことになる。
「Nの補数」は「対象の数の最大の桁+1桁が1、それ以降の桁が0の数から対象の値を引いた値」を指す。
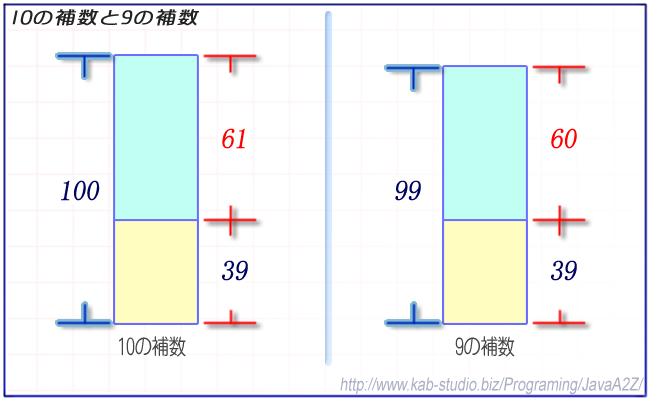
10進数の「10の補数」を求める場合、「39」であれば「対象の数の最大の桁+1桁が1、それ以降の桁が0の数」は「100」であり、この数から引いた「61」が「10の補数」ということになる。
「N-1の補数」は「対象の数の各桁を、N-1から引いた値」を指す。
10進数の「9の補数」を求める場合、「39」であれば「対象の数の各桁を、N-1から引いた値」は、各桁を「9」から引いた値「60」が「9の補数」ということになる。
一般によく使われるのは「Nの補数」の方である。
これは、「Nの補数」が「足し算だけで引き算が可能になる」ためである。
Nの補数はそれそのものがマイナスの意味を持ち、足し算で引き算を計算することができる。
たとえば51 - 39 = 12を計算する場合、先ほどの10の補数より51 + 61 = 112、一番上の桁を無視すればこれが答の12と一致していることがわかる。
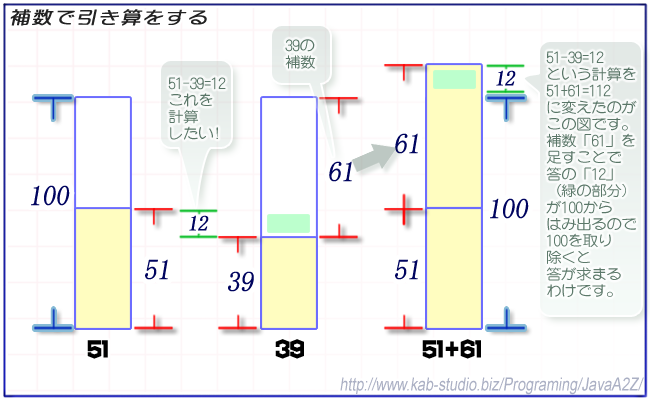
この「一番上の桁を無視する」というのが重要である。この無視する部分を含めて計算すると51 - 39 = 51 + ( 61 - 100 ) = 12となる。つまり「一番上の桁を無視する」ということが「-100する」という計算を意味しており、このトリックで「足し算で引き算を計算する」とみせかけている。さらに言えば、補数を作ること自体が引き算であり、結局引き算を使わなければ足し算はできないことになる。
ただし、2の補数をコンピューターで作成する場合、ビットの反転等で作ることができる。コンピューターで引き算をする場合には専用の回路を用意する必要があり、その回路を作らずに済ませるため、2の補数を用いて足し算の回路で引き算を行っている。
そのため、コンピューターでは整数の負の値を2の補数で表現している。詳しくは「2の補数」を参照のこと。
ある数の「逆の数」「補う数」のこと。たとえば10進数の場合「3」の補数は「7」であり、「39」の補数は「61」である。

正確には、補数には「Nの補数」と「N-1の補数」の2種類がある。
「N」には、対象の数の進数が入る。10進数であれば「10の補数」と「9の補数」があり、2進数であれば「2の補数」と「1の補数」がある。
そのため、たとえば10進数において「8の補数」等は存在しないことになる。
「Nの補数」は「対象の数の最大の桁+1桁が1、それ以降の桁が0の数から対象の値を引いた値」を指す。
10進数の「10の補数」を求める場合、「39」であれば「対象の数の最大の桁+1桁が1、それ以降の桁が0の数」は「100」であり、この数から引いた「61」が「10の補数」ということになる。
「N-1の補数」は「対象の数の各桁を、N-1から引いた値」を指す。
10進数の「9の補数」を求める場合、「39」であれば「対象の数の各桁を、N-1から引いた値」は、各桁を「9」から引いた値「60」が「9の補数」ということになる。

一般によく使われるのは「Nの補数」の方である。
これは、「Nの補数」が「足し算だけで引き算が可能になる」ためである。
Nの補数はそれそのものがマイナスの意味を持ち、足し算で引き算を計算することができる。
たとえば51 - 39 = 12を計算する場合、先ほどの10の補数より51 + 61 = 112、一番上の桁を無視すればこれが答の12と一致していることがわかる。

この「一番上の桁を無視する」というのが重要である。この無視する部分を含めて計算すると51 - 39 = 51 + ( 61 - 100 ) = 12となる。つまり「一番上の桁を無視する」ということが「-100する」という計算を意味しており、このトリックで「足し算で引き算を計算する」とみせかけている。さらに言えば、補数を作ること自体が引き算であり、結局引き算を使わなければ足し算はできないことになる。
ただし、2の補数をコンピューターで作成する場合、ビットの反転等で作ることができる。コンピューターで引き算をする場合には専用の回路を用意する必要があり、その回路を作らずに済ませるため、2の補数を用いて足し算の回路で引き算を行っている。
そのため、コンピューターでは整数の負の値を2の補数で表現している。詳しくは「2の補数」を参照のこと。
参考サイト
- (参考サイトはありません)
「補数って難しいよね……」
「いや、別に難しくないっしょ。ビット反転して1足す。つかマイナスの数をビットで見まくれば分かってくるし」
「2の補数はな……基本情報技術者試験とか大学の授業とかだと、10の補数や1の補数なんかもちゃんと理解してないと問題解けないから」
「あー、そういうの……」
「なのに先生、ちゃんと説明しないから8の補数や7の補数があると思ってたし……ああ、なんかトラウマが……」
「いや、別に難しくないっしょ。ビット反転して1足す。つかマイナスの数をビットで見まくれば分かってくるし」
「2の補数はな……基本情報技術者試験とか大学の授業とかだと、10の補数や1の補数なんかもちゃんと理解してないと問題解けないから」
「あー、そういうの……」
「なのに先生、ちゃんと説明しないから8の補数や7の補数があると思ってたし……ああ、なんかトラウマが……」
「補数って難しいよね……」 「いや、別に難しくないっしょ。ビット反転して1足す。つかマイナスの数をビットで見まくれば分かってくるし」 「2の補数はな……基本情報技術者試験とか大学の授業とかだと、10の補数や1の補数なんかもちゃんと理解してないと問題解けないから」 「あー、そういうの……」 「なのに先生、ちゃんと説明しないから8の補数や7の補数があると思ってたし……ああ、なんかトラウマが……」






