仮数部
| 日本語 | 浮動小数点の分数の部分 |
| 英語 | mantissa |
| ふりがな | かすうぶ |
| フリガナ | カスウブ |
浮動小数点の中の「指数部の間を埋める」ための部分。
double型の場合、全64ビットの内、12ビット目以降(左端のビットを0ビット目とした場合)が仮数部となる。
float型の場合、全32ビットの内、9ビット目以降(左端のビットを0ビット目とした場合)が仮数部となる。

以下、double型における、浮動小数点の仮数部について説明する。
指数部には「2の累乗」、つまり2、4、8、16...といった「おおざっぱな飛び飛びの値」が格納されている。
仮数部はこの「おおざっぱな飛び飛びの値」の間を埋めるためのものである。
仮数部はビット毎に1/2、1/4、1/8...といった値を持つ。それら全てを足したものに1を足した値が「仮数部としての値」となる。
仮数部の値は、全てのビットが0であれば「0 + 0 + 0 + 0 ... + 1 = 1」となる。また、全てのビットが1であれば「1/2 + 1/4 + 1/8 + ... + 1 = 1.99999...」という値になる。つまり、仮数部は「1以上2未満」の値を表現することができる。
浮動小数点は、この仮数部と、指数部を掛けたものである。
指数部の「2の累乗」は、仮数部の「1以上2未満」を掛ける事によって、「飛び飛びの値」の「間の値」となる。
この、指数部と仮数部を掛けた値が実際の値となる。
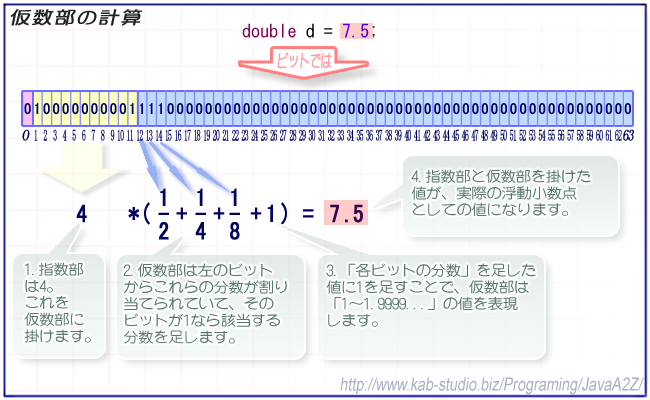
これはつまり、仮数部は「指数部の飛び飛びの値」の「中間の値」を指すためのもの、ということである。
指数部が「4」の時に、仮数部は「4以上8未満の値」を指すために使用する。たとえば、仮数部が「100000...」の時の値は「6」、仮数部が「010000...」の時の値は「5」、仮数部が「001000...」の時の値は「4.5」となる。
つまり仮数部は、指数部の「4以上8未満の間」を「2分の1」していくことで、目的の値を作りだす。
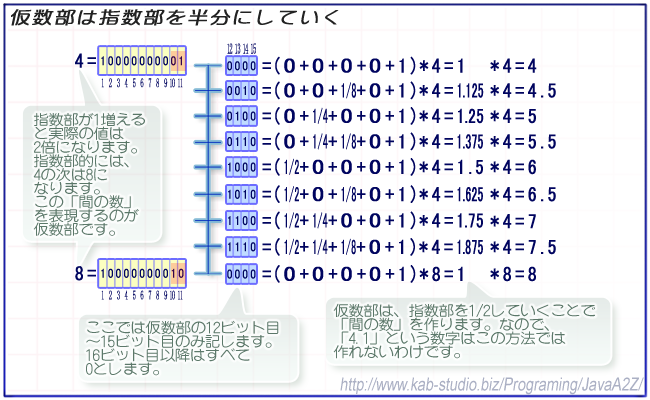
言い換えると、仮数部は「2で割ることしかできない」ということである。
そのため、仮数部で表現する「1以上2未満」の値のうち、あらゆる値を表現できるわけではない。
たとえば「4.1」という値を表現することはできない。「4以上8未満」の間で「2分の1」を繰り返したとしても「4.1」にはならず、近似値にしかならないためである。
結果、浮動小数点は「正確な値」を表現することには向いてないということになる。
浮動小数点は、誤差があっても構わない計算にのみ使用し、正確な値が必要な場合はBigDecimalクラスを使用した方がいいだろう。
double型の場合、全64ビットの内、12ビット目以降(左端のビットを0ビット目とした場合)が仮数部となる。
float型の場合、全32ビットの内、9ビット目以降(左端のビットを0ビット目とした場合)が仮数部となる。

以下、double型における、浮動小数点の仮数部について説明する。
指数部には「2の累乗」、つまり2、4、8、16...といった「おおざっぱな飛び飛びの値」が格納されている。
仮数部はこの「おおざっぱな飛び飛びの値」の間を埋めるためのものである。
仮数部はビット毎に1/2、1/4、1/8...といった値を持つ。それら全てを足したものに1を足した値が「仮数部としての値」となる。
仮数部の値は、全てのビットが0であれば「0 + 0 + 0 + 0 ... + 1 = 1」となる。また、全てのビットが1であれば「1/2 + 1/4 + 1/8 + ... + 1 = 1.99999...」という値になる。つまり、仮数部は「1以上2未満」の値を表現することができる。
浮動小数点は、この仮数部と、指数部を掛けたものである。
指数部の「2の累乗」は、仮数部の「1以上2未満」を掛ける事によって、「飛び飛びの値」の「間の値」となる。
この、指数部と仮数部を掛けた値が実際の値となる。

これはつまり、仮数部は「指数部の飛び飛びの値」の「中間の値」を指すためのもの、ということである。
指数部が「4」の時に、仮数部は「4以上8未満の値」を指すために使用する。たとえば、仮数部が「100000...」の時の値は「6」、仮数部が「010000...」の時の値は「5」、仮数部が「001000...」の時の値は「4.5」となる。
つまり仮数部は、指数部の「4以上8未満の間」を「2分の1」していくことで、目的の値を作りだす。

言い換えると、仮数部は「2で割ることしかできない」ということである。
そのため、仮数部で表現する「1以上2未満」の値のうち、あらゆる値を表現できるわけではない。
たとえば「4.1」という値を表現することはできない。「4以上8未満」の間で「2分の1」を繰り返したとしても「4.1」にはならず、近似値にしかならないためである。
結果、浮動小数点は「正確な値」を表現することには向いてないということになる。
浮動小数点は、誤差があっても構わない計算にのみ使用し、正確な値が必要な場合はBigDecimalクラスを使用した方がいいだろう。
// Sample.java
import java.text.DecimalFormat;
public class Sample
{
public static void main( String[] args )
{
// 浮動小数点で一番「普通」の値は「2.0」です。
outputDoubleBit( 2.0 );
// 0 10000000000 0000000000000000000000000000000000000000000000000000
// ←指数部 → ←仮数部 →
// 12ビット目以降には仮数部が格納されます。
outputDoubleBit( 7.5 );
// 0 10000000001 1110000000000000000000000000000000000000000000000000
// 仮数部のビットは、左から1、2、3...という値が割り振られて
// いると考えてください。
// そして、そのビットが1だと「2の-(そのビットの数)乗」
// という値が得られると考えてください。
// たとえば、一番左は2の-1乗 = 1/2 = 0.5、
// その次は2の-2乗 = 1/4 = 0.25、
// その次は2の-3乗 = 1/8 = 0.125、となります。
// 仮数部は、これらの値の和に1を足したものになります。
// この例だと0.5 + 0.25 + 0.125 + 1 = 1.875になります。
// これに指数部の4を掛けると、実際の値、7.5になる
// というわけです。
// 仮数部は、指数部の「間を埋める」ためのものです。
outputDoubleBit( 1.0 );
outputDoubleBit( 1.25 );
outputDoubleBit( 1.5 );
outputDoubleBit( 1.75 );
outputDoubleBit( 2.0 );
// 0 01111111111 0000000000000000000000000000000000000000000000000000
// 0 01111111111 0100000000000000000000000000000000000000000000000000
// 0 01111111111 1000000000000000000000000000000000000000000000000000
// 0 01111111111 1100000000000000000000000000000000000000000000000000
// 0 10000000000 0000000000000000000000000000000000000000000000000000
// 仮数部は「2の分数+1」なので、どんなに足しても
// 「1以上2未満」にしかなりません。
// これが「指数部の間を埋める」ために必要なことです。
// 「1以上2未満」であれば、どんな大きな値を「2の乗数」
// に掛けても、絶対に「2の(+1乗数)」にはなりませんし、
// どんな小さな値を「2の乗数」に掛けてもその「2の乗数」
// より減る事はありません。
// これを10進数で考えると、仮数部は「0以上10未満」の値を
// 表すということで、浮動小数点的にも「仮数部が実際の値、
// 指数部が小数点の位置」、という役割を果たしていると
// 言えるわけです。
// 仮数部は、あくまで「2の分数」、つまり「2で割る」こと
// しかできません。
outputDoubleBit( 4.0 );
outputDoubleBit( 4.5 );
outputDoubleBit( 5.0 );
outputDoubleBit( 5.5 );
outputDoubleBit( 6.0 );
outputDoubleBit( 6.5 );
outputDoubleBit( 7.0 );
outputDoubleBit( 7.5 );
outputDoubleBit( 8.0 );
// 0 10000000001 0000000000000000000000000000000000000000000000000000
// 0 10000000001 0010000000000000000000000000000000000000000000000000
// 0 10000000001 0100000000000000000000000000000000000000000000000000
// 0 10000000001 0110000000000000000000000000000000000000000000000000
// 0 10000000001 1000000000000000000000000000000000000000000000000000
// 0 10000000001 1010000000000000000000000000000000000000000000000000
// 0 10000000001 1100000000000000000000000000000000000000000000000000
// 0 10000000001 1110000000000000000000000000000000000000000000000000
// 0 10000000010 0000000000000000000000000000000000000000000000000000
// 仮数部は「2の分数」なので、指数部の間の数
// (この例だと4~8の間の数)全てを表現することはできません。
// そのため、「4.1」なんていうごく普通の値すら正確には
// 表現できません。
outputDoubleBit( 4.1 );
// 0 10000000001 0000011001100110011001100110011001100110011001100110
// この値は「4.1の近似値」であり、正確には「4.1」では
// ありません。
// たとえば、4.1 + 8.2を計算すると、12.3になりません。
String format = "0.00000000000000000000000000000000000000000000000000";
DecimalFormat decimalFormat = new DecimalFormat( format );
System.out.println( decimalFormat.format( 4.1 + 8.2 ) );
// 12.29999999999999900000000000000000000000000000000000
// このように、浮動小数点は「正確な値を表現する」目的には
// 使用できません。
// 代わりにBigDecimalクラスを使用しましょう。
}
/**
* double型変数をビット形式で出力します。
*/
private static void outputDoubleBit( double d )
{
// double型変数をビット形式で文字列化します。
String source = Long.toBinaryString( Double.doubleToLongBits( d ) );
// 左0埋めします。
StringBuffer strbuf = new StringBuffer();
for( int iF1 = source.length(); iF1 < 64; ++iF1 )
{
strbuf.append( "0" );
}
strbuf.append( source );
// 符号、仮数部、指数部の間にスペースを入れます。
strbuf.insert( 12, " " );
strbuf.insert( 1, " " );
System.out.println( strbuf.toString() );
}
}
import java.text.DecimalFormat;
public class Sample
{
public static void main( String[] args )
{
// 浮動小数点で一番「普通」の値は「2.0」です。
outputDoubleBit( 2.0 );
// 0 10000000000 0000000000000000000000000000000000000000000000000000
// ←指数部 → ←仮数部 →
// 12ビット目以降には仮数部が格納されます。
outputDoubleBit( 7.5 );
// 0 10000000001 1110000000000000000000000000000000000000000000000000
// 仮数部のビットは、左から1、2、3...という値が割り振られて
// いると考えてください。
// そして、そのビットが1だと「2の-(そのビットの数)乗」
// という値が得られると考えてください。
// たとえば、一番左は2の-1乗 = 1/2 = 0.5、
// その次は2の-2乗 = 1/4 = 0.25、
// その次は2の-3乗 = 1/8 = 0.125、となります。
// 仮数部は、これらの値の和に1を足したものになります。
// この例だと0.5 + 0.25 + 0.125 + 1 = 1.875になります。
// これに指数部の4を掛けると、実際の値、7.5になる
// というわけです。
// 仮数部は、指数部の「間を埋める」ためのものです。
outputDoubleBit( 1.0 );
outputDoubleBit( 1.25 );
outputDoubleBit( 1.5 );
outputDoubleBit( 1.75 );
outputDoubleBit( 2.0 );
// 0 01111111111 0000000000000000000000000000000000000000000000000000
// 0 01111111111 0100000000000000000000000000000000000000000000000000
// 0 01111111111 1000000000000000000000000000000000000000000000000000
// 0 01111111111 1100000000000000000000000000000000000000000000000000
// 0 10000000000 0000000000000000000000000000000000000000000000000000
// 仮数部は「2の分数+1」なので、どんなに足しても
// 「1以上2未満」にしかなりません。
// これが「指数部の間を埋める」ために必要なことです。
// 「1以上2未満」であれば、どんな大きな値を「2の乗数」
// に掛けても、絶対に「2の(+1乗数)」にはなりませんし、
// どんな小さな値を「2の乗数」に掛けてもその「2の乗数」
// より減る事はありません。
// これを10進数で考えると、仮数部は「0以上10未満」の値を
// 表すということで、浮動小数点的にも「仮数部が実際の値、
// 指数部が小数点の位置」、という役割を果たしていると
// 言えるわけです。
// 仮数部は、あくまで「2の分数」、つまり「2で割る」こと
// しかできません。
outputDoubleBit( 4.0 );
outputDoubleBit( 4.5 );
outputDoubleBit( 5.0 );
outputDoubleBit( 5.5 );
outputDoubleBit( 6.0 );
outputDoubleBit( 6.5 );
outputDoubleBit( 7.0 );
outputDoubleBit( 7.5 );
outputDoubleBit( 8.0 );
// 0 10000000001 0000000000000000000000000000000000000000000000000000
// 0 10000000001 0010000000000000000000000000000000000000000000000000
// 0 10000000001 0100000000000000000000000000000000000000000000000000
// 0 10000000001 0110000000000000000000000000000000000000000000000000
// 0 10000000001 1000000000000000000000000000000000000000000000000000
// 0 10000000001 1010000000000000000000000000000000000000000000000000
// 0 10000000001 1100000000000000000000000000000000000000000000000000
// 0 10000000001 1110000000000000000000000000000000000000000000000000
// 0 10000000010 0000000000000000000000000000000000000000000000000000
// 仮数部は「2の分数」なので、指数部の間の数
// (この例だと4~8の間の数)全てを表現することはできません。
// そのため、「4.1」なんていうごく普通の値すら正確には
// 表現できません。
outputDoubleBit( 4.1 );
// 0 10000000001 0000011001100110011001100110011001100110011001100110
// この値は「4.1の近似値」であり、正確には「4.1」では
// ありません。
// たとえば、4.1 + 8.2を計算すると、12.3になりません。
String format = "0.00000000000000000000000000000000000000000000000000";
DecimalFormat decimalFormat = new DecimalFormat( format );
System.out.println( decimalFormat.format( 4.1 + 8.2 ) );
// 12.29999999999999900000000000000000000000000000000000
// このように、浮動小数点は「正確な値を表現する」目的には
// 使用できません。
// 代わりにBigDecimalクラスを使用しましょう。
}
/**
* double型変数をビット形式で出力します。
*/
private static void outputDoubleBit( double d )
{
// double型変数をビット形式で文字列化します。
String source = Long.toBinaryString( Double.doubleToLongBits( d ) );
// 左0埋めします。
StringBuffer strbuf = new StringBuffer();
for( int iF1 = source.length(); iF1 < 64; ++iF1 )
{
strbuf.append( "0" );
}
strbuf.append( source );
// 符号、仮数部、指数部の間にスペースを入れます。
strbuf.insert( 12, " " );
strbuf.insert( 1, " " );
System.out.println( strbuf.toString() );
}
}
// Sample.java
import java.text.DecimalFormat;
public class Sample
{
public static void main( String[] args )
{
// 浮動小数点で一番「普通」の値は「2.0」です。
outputDoubleBit( 2.0 );
// 0 10000000000 0000000000000000000000000000000000000000000000000000
// ←指数部 → ←仮数部 →
// 12ビット目以降には仮数部が格納されます。
outputDoubleBit( 7.5 );
// 0 10000000001 1110000000000000000000000000000000000000000000000000
// 仮数部のビットは、左から1、2、3...という値が割り振られて
// いると考えてください。
// そして、そのビットが1だと「2の-(そのビットの数)乗」
// という値が得られると考えてください。
// たとえば、一番左は2の-1乗 = 1/2 = 0.5、
// その次は2の-2乗 = 1/4 = 0.25、
// その次は2の-3乗 = 1/8 = 0.125、となります。
// 仮数部は、これらの値の和に1を足したものになります。
// この例だと0.5 + 0.25 + 0.125 + 1 = 1.875になります。
// これに指数部の4を掛けると、実際の値、7.5になる
// というわけです。
// 仮数部は、指数部の「間を埋める」ためのものです。
outputDoubleBit( 1.0 );
outputDoubleBit( 1.25 );
outputDoubleBit( 1.5 );
outputDoubleBit( 1.75 );
outputDoubleBit( 2.0 );
// 0 01111111111 0000000000000000000000000000000000000000000000000000
// 0 01111111111 0100000000000000000000000000000000000000000000000000
// 0 01111111111 1000000000000000000000000000000000000000000000000000
// 0 01111111111 1100000000000000000000000000000000000000000000000000
// 0 10000000000 0000000000000000000000000000000000000000000000000000
// 仮数部は「2の分数+1」なので、どんなに足しても
// 「1以上2未満」にしかなりません。
// これが「指数部の間を埋める」ために必要なことです。
// 「1以上2未満」であれば、どんな大きな値を「2の乗数」
// に掛けても、絶対に「2の(+1乗数)」にはなりませんし、
// どんな小さな値を「2の乗数」に掛けてもその「2の乗数」
// より減る事はありません。
// これを10進数で考えると、仮数部は「0以上10未満」の値を
// 表すということで、浮動小数点的にも「仮数部が実際の値、
// 指数部が小数点の位置」、という役割を果たしていると
// 言えるわけです。
// 仮数部は、あくまで「2の分数」、つまり「2で割る」こと
// しかできません。
outputDoubleBit( 4.0 );
outputDoubleBit( 4.5 );
outputDoubleBit( 5.0 );
outputDoubleBit( 5.5 );
outputDoubleBit( 6.0 );
outputDoubleBit( 6.5 );
outputDoubleBit( 7.0 );
outputDoubleBit( 7.5 );
outputDoubleBit( 8.0 );
// 0 10000000001 0000000000000000000000000000000000000000000000000000
// 0 10000000001 0010000000000000000000000000000000000000000000000000
// 0 10000000001 0100000000000000000000000000000000000000000000000000
// 0 10000000001 0110000000000000000000000000000000000000000000000000
// 0 10000000001 1000000000000000000000000000000000000000000000000000
// 0 10000000001 1010000000000000000000000000000000000000000000000000
// 0 10000000001 1100000000000000000000000000000000000000000000000000
// 0 10000000001 1110000000000000000000000000000000000000000000000000
// 0 10000000010 0000000000000000000000000000000000000000000000000000
// 仮数部は「2の分数」なので、指数部の間の数
// (この例だと4~8の間の数)全てを表現することはできません。
// そのため、「4.1」なんていうごく普通の値すら正確には
// 表現できません。
outputDoubleBit( 4.1 );
// 0 10000000001 0000011001100110011001100110011001100110011001100110
// この値は「4.1の近似値」であり、正確には「4.1」では
// ありません。
// たとえば、4.1 + 8.2を計算すると、12.3になりません。
String format = "0.00000000000000000000000000000000000000000000000000";
DecimalFormat decimalFormat = new DecimalFormat( format );
System.out.println( decimalFormat.format( 4.1 + 8.2 ) );
// 12.29999999999999900000000000000000000000000000000000
// このように、浮動小数点は「正確な値を表現する」目的には
// 使用できません。
// 代わりにBigDecimalクラスを使用しましょう。
}
/**
* double型変数をビット形式で出力します。
*/
private static void outputDoubleBit( double d )
{
// double型変数をビット形式で文字列化します。
String source = Long.toBinaryString( Double.doubleToLongBits( d ) );
// 左0埋めします。
StringBuffer strbuf = new StringBuffer();
for( int iF1 = source.length(); iF1 < 64; ++iF1 )
{
strbuf.append( "0" );
}
strbuf.append( source );
// 符号、仮数部、指数部の間にスペースを入れます。
strbuf.insert( 12, " " );
strbuf.insert( 1, " " );
System.out.println( strbuf.toString() );
}
}






