浮動小数点
| 日本語 | 小数点が移動する実数 |
| 英語 | floating-point number |
| ふりがな | ふどうしょうすうてん |
| フリガナ | フドウショウスウテン |
実数の表現方法のひとつ。
float型やdouble型が採用している、実数値の格納方法。
IEEE754という国際規格に則っている。
以下、double型の浮動小数点について説明する。
浮動小数点では、変数全体の64ビットの内、3つに分割して使用している。一番左のビットを0番目のビットとした場合、以下のように割り振られている。
・0ビット目:符号
・1ビット目~11ビット目:指数部
・12ビット目~63ビット目:仮数部
「符号」はその名の通りプラスかマイナスを格納する。0がプラス、1がマイナスを表す。
「指数部」は「2の累乗」を格納する。たとえば「16.0」の場合、「2の4乗」のため「4」を示す値が格納される。
「仮数部」は「有効な値」を格納する。指数部は「2の累乗」というおおざっぱな値のため、その間を埋める値として仮数部がある。
実際の値は「指数部*仮数部」に符号を付けたものとなる。
詳しくは「指数部」「仮数部」の項目を参照。
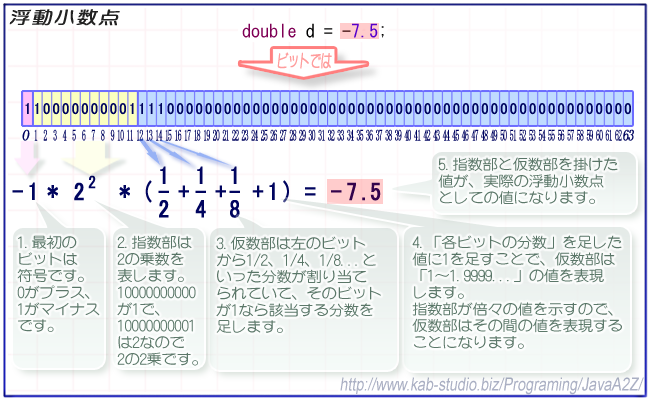
名称としての「浮動小数点」からは、10進数表記で「小数点が移動する」イメージがあるが、そのイメージは捨てた方がよい。
「指数部」は「2の累乗」によって表現される。乗数は-1023~1023の値が使用できる。
ここで、10進数の場合を考えてみる。10進数の場合、100は10の2乗、1000は10の3乗、0.1は10の-1乗、0.01は10の-2乗と表現できる。つまり10進数の場合、10の累乗が「小数点の位置」を決めているということになる。
これが、指数部の「2進数」にも当てはまる。指数部は2の累乗を表しており、これが2進数での「小数点の位置」を表している。指数部の値によって小数点が移動する、これが「浮動小数点」の由来である。
浮動小数点は、基本的に「おおざっぱな値」であり、常に正確な値を表現しているとは限らない。
これは、仮数部の性質による。仮数部は「指数部を割るための分数」である。たとえば「6.0」という値を表現する場合、指数部では「2の累乗」で表現できる「8」、仮数部は「指数部を割るための分数」として「3/4」、このふたつを掛けて「6」という値を表現する。
このように、仮数部は「指数部を割るための分数」であり、その性質上、たとえば「6.1」という値を正確に表現することは不可能である。これを「丸め誤差」という。
この性質故、浮動小数点は「誤差が許される近似値の計算」にのみ使用することが可能であり、計算機の元々の目的である「物理計算」や、正確な値よりも高速な演算が求められる3DCGなどでは使用してもよいが、通常の実数計算、特に貨幣計算には絶対に使用してはならない。
BigDecimalクラスという「丸め誤差を生まない実数を格納するクラス」が存在するため、正確な値が必要な場合にはこちらを使用した方がいいだろう。
float型やdouble型が採用している、実数値の格納方法。
IEEE754という国際規格に則っている。
以下、double型の浮動小数点について説明する。
浮動小数点では、変数全体の64ビットの内、3つに分割して使用している。一番左のビットを0番目のビットとした場合、以下のように割り振られている。
・0ビット目:符号
・1ビット目~11ビット目:指数部
・12ビット目~63ビット目:仮数部
「符号」はその名の通りプラスかマイナスを格納する。0がプラス、1がマイナスを表す。
「指数部」は「2の累乗」を格納する。たとえば「16.0」の場合、「2の4乗」のため「4」を示す値が格納される。
「仮数部」は「有効な値」を格納する。指数部は「2の累乗」というおおざっぱな値のため、その間を埋める値として仮数部がある。
実際の値は「指数部*仮数部」に符号を付けたものとなる。
詳しくは「指数部」「仮数部」の項目を参照。

名称としての「浮動小数点」からは、10進数表記で「小数点が移動する」イメージがあるが、そのイメージは捨てた方がよい。
「指数部」は「2の累乗」によって表現される。乗数は-1023~1023の値が使用できる。
ここで、10進数の場合を考えてみる。10進数の場合、100は10の2乗、1000は10の3乗、0.1は10の-1乗、0.01は10の-2乗と表現できる。つまり10進数の場合、10の累乗が「小数点の位置」を決めているということになる。
これが、指数部の「2進数」にも当てはまる。指数部は2の累乗を表しており、これが2進数での「小数点の位置」を表している。指数部の値によって小数点が移動する、これが「浮動小数点」の由来である。
浮動小数点は、基本的に「おおざっぱな値」であり、常に正確な値を表現しているとは限らない。
これは、仮数部の性質による。仮数部は「指数部を割るための分数」である。たとえば「6.0」という値を表現する場合、指数部では「2の累乗」で表現できる「8」、仮数部は「指数部を割るための分数」として「3/4」、このふたつを掛けて「6」という値を表現する。
このように、仮数部は「指数部を割るための分数」であり、その性質上、たとえば「6.1」という値を正確に表現することは不可能である。これを「丸め誤差」という。
この性質故、浮動小数点は「誤差が許される近似値の計算」にのみ使用することが可能であり、計算機の元々の目的である「物理計算」や、正確な値よりも高速な演算が求められる3DCGなどでは使用してもよいが、通常の実数計算、特に貨幣計算には絶対に使用してはならない。
BigDecimalクラスという「丸め誤差を生まない実数を格納するクラス」が存在するため、正確な値が必要な場合にはこちらを使用した方がいいだろう。
// Sample.java
import java.text.DecimalFormat;
public class Sample
{
public static void main( String[] args )
{
// 浮動小数点で一番「普通」の値は「2.0」です。
// double型の場合、この値の各ビットは以下のようになります。
outputDoubleBit( 2.0 );
// 0 10000000000 0000000000000000000000000000000000000000000000000000
// マイナスの場合は0番目のビットが1になります。
outputDoubleBit( -2.0 );
// 1 10000000000 0000000000000000000000000000000000000000000000000000
// 1ビット目~11ビット目は指数部、2の累乗が格納されます。
outputDoubleBit( 0.125 );
outputDoubleBit( 0.25 );
outputDoubleBit( 0.5 );
outputDoubleBit( 1.0 );
outputDoubleBit( 2.0 );
outputDoubleBit( 4.0 );
outputDoubleBit( 8.0 );
outputDoubleBit( 16.0 );
// 0 01111111100 0000000000000000000000000000000000000000000000000000
// 0 01111111101 0000000000000000000000000000000000000000000000000000
// 0 01111111110 0000000000000000000000000000000000000000000000000000
// 0 01111111111 0000000000000000000000000000000000000000000000000000
// 0 10000000000 0000000000000000000000000000000000000000000000000000
// 0 10000000001 0000000000000000000000000000000000000000000000000000
// 0 10000000010 0000000000000000000000000000000000000000000000000000
// 0 10000000011 0000000000000000000000000000000000000000000000000000
// 指数のビットは、整数とほぼ同じです。
// ただし、2の-1023乗の時に00000000000、
// 2の1023乗の時に11111111111となります。
// 残りのビットには仮数部が格納されます。
outputDoubleBit( 4.0 );
outputDoubleBit( 4.5 );
outputDoubleBit( 5.0 );
outputDoubleBit( 5.5 );
outputDoubleBit( 6.0 );
outputDoubleBit( 6.5 );
outputDoubleBit( 7.0 );
outputDoubleBit( 7.5 );
outputDoubleBit( 8.0 );
// 0 10000000001 0000000000000000000000000000000000000000000000000000
// 0 10000000001 0010000000000000000000000000000000000000000000000000
// 0 10000000001 0100000000000000000000000000000000000000000000000000
// 0 10000000001 0110000000000000000000000000000000000000000000000000
// 0 10000000001 1000000000000000000000000000000000000000000000000000
// 0 10000000001 1010000000000000000000000000000000000000000000000000
// 0 10000000001 1100000000000000000000000000000000000000000000000000
// 0 10000000001 1110000000000000000000000000000000000000000000000000
// 0 10000000010 0000000000000000000000000000000000000000000000000000
// 仮数部は、左から0.5、0.25、0.125を意味します。
// この仮数部を足した値+1を指数部に掛けたものが結果になります。
// 仮数部は「2の分数」なので、指数部の間の数(この例だと4~8の間の数)
// 全てを表現することはできません。
// そのため、「4.1」なんていうごく普通の値すら正確には表現できません。
outputDoubleBit( 4.1 );
// 0 10000000001 0000011001100110011001100110011001100110011001100110
// この値は「4.1の近似値」であり、正確には「4.1」ではありません。
// たとえば、4.1 + 8.2を計算すると、12.3になりません。
String format = "0.00000000000000000000000000000000000000000000000000";
DecimalFormat decimalFormat = new DecimalFormat( format );
System.out.println( decimalFormat.format( 4.1 + 8.2 ) );
// 12.29999999999999900000000000000000000000000000000000
// このように、浮動小数点は「正確な値を表現する」目的には使用できません。
// BigDecimalクラスを使用するようにしましょう。
}
/**
* double型変数をビット形式で出力します。
*/
private static void outputDoubleBit( double d )
{
// double型変数をビット形式で文字列化します。
String source = Long.toBinaryString( Double.doubleToLongBits( d ) );
// 左0埋めします。
StringBuffer strbuf = new StringBuffer();
for( int iF1 = source.length(); iF1 < 64; ++iF1 )
{
strbuf.append( "0" );
}
strbuf.append( source );
// 符号、仮数部、指数部の間にスペースを入れます。
strbuf.insert( 12, " " );
strbuf.insert( 1, " " );
System.out.println( strbuf.toString() );
}
}
import java.text.DecimalFormat;
public class Sample
{
public static void main( String[] args )
{
// 浮動小数点で一番「普通」の値は「2.0」です。
// double型の場合、この値の各ビットは以下のようになります。
outputDoubleBit( 2.0 );
// 0 10000000000 0000000000000000000000000000000000000000000000000000
// マイナスの場合は0番目のビットが1になります。
outputDoubleBit( -2.0 );
// 1 10000000000 0000000000000000000000000000000000000000000000000000
// 1ビット目~11ビット目は指数部、2の累乗が格納されます。
outputDoubleBit( 0.125 );
outputDoubleBit( 0.25 );
outputDoubleBit( 0.5 );
outputDoubleBit( 1.0 );
outputDoubleBit( 2.0 );
outputDoubleBit( 4.0 );
outputDoubleBit( 8.0 );
outputDoubleBit( 16.0 );
// 0 01111111100 0000000000000000000000000000000000000000000000000000
// 0 01111111101 0000000000000000000000000000000000000000000000000000
// 0 01111111110 0000000000000000000000000000000000000000000000000000
// 0 01111111111 0000000000000000000000000000000000000000000000000000
// 0 10000000000 0000000000000000000000000000000000000000000000000000
// 0 10000000001 0000000000000000000000000000000000000000000000000000
// 0 10000000010 0000000000000000000000000000000000000000000000000000
// 0 10000000011 0000000000000000000000000000000000000000000000000000
// 指数のビットは、整数とほぼ同じです。
// ただし、2の-1023乗の時に00000000000、
// 2の1023乗の時に11111111111となります。
// 残りのビットには仮数部が格納されます。
outputDoubleBit( 4.0 );
outputDoubleBit( 4.5 );
outputDoubleBit( 5.0 );
outputDoubleBit( 5.5 );
outputDoubleBit( 6.0 );
outputDoubleBit( 6.5 );
outputDoubleBit( 7.0 );
outputDoubleBit( 7.5 );
outputDoubleBit( 8.0 );
// 0 10000000001 0000000000000000000000000000000000000000000000000000
// 0 10000000001 0010000000000000000000000000000000000000000000000000
// 0 10000000001 0100000000000000000000000000000000000000000000000000
// 0 10000000001 0110000000000000000000000000000000000000000000000000
// 0 10000000001 1000000000000000000000000000000000000000000000000000
// 0 10000000001 1010000000000000000000000000000000000000000000000000
// 0 10000000001 1100000000000000000000000000000000000000000000000000
// 0 10000000001 1110000000000000000000000000000000000000000000000000
// 0 10000000010 0000000000000000000000000000000000000000000000000000
// 仮数部は、左から0.5、0.25、0.125を意味します。
// この仮数部を足した値+1を指数部に掛けたものが結果になります。
// 仮数部は「2の分数」なので、指数部の間の数(この例だと4~8の間の数)
// 全てを表現することはできません。
// そのため、「4.1」なんていうごく普通の値すら正確には表現できません。
outputDoubleBit( 4.1 );
// 0 10000000001 0000011001100110011001100110011001100110011001100110
// この値は「4.1の近似値」であり、正確には「4.1」ではありません。
// たとえば、4.1 + 8.2を計算すると、12.3になりません。
String format = "0.00000000000000000000000000000000000000000000000000";
DecimalFormat decimalFormat = new DecimalFormat( format );
System.out.println( decimalFormat.format( 4.1 + 8.2 ) );
// 12.29999999999999900000000000000000000000000000000000
// このように、浮動小数点は「正確な値を表現する」目的には使用できません。
// BigDecimalクラスを使用するようにしましょう。
}
/**
* double型変数をビット形式で出力します。
*/
private static void outputDoubleBit( double d )
{
// double型変数をビット形式で文字列化します。
String source = Long.toBinaryString( Double.doubleToLongBits( d ) );
// 左0埋めします。
StringBuffer strbuf = new StringBuffer();
for( int iF1 = source.length(); iF1 < 64; ++iF1 )
{
strbuf.append( "0" );
}
strbuf.append( source );
// 符号、仮数部、指数部の間にスペースを入れます。
strbuf.insert( 12, " " );
strbuf.insert( 1, " " );
System.out.println( strbuf.toString() );
}
}
// Sample.java
import java.text.DecimalFormat;
public class Sample
{
public static void main( String[] args )
{
// 浮動小数点で一番「普通」の値は「2.0」です。
// double型の場合、この値の各ビットは以下のようになります。
outputDoubleBit( 2.0 );
// 0 10000000000 0000000000000000000000000000000000000000000000000000
// マイナスの場合は0番目のビットが1になります。
outputDoubleBit( -2.0 );
// 1 10000000000 0000000000000000000000000000000000000000000000000000
// 1ビット目~11ビット目は指数部、2の累乗が格納されます。
outputDoubleBit( 0.125 );
outputDoubleBit( 0.25 );
outputDoubleBit( 0.5 );
outputDoubleBit( 1.0 );
outputDoubleBit( 2.0 );
outputDoubleBit( 4.0 );
outputDoubleBit( 8.0 );
outputDoubleBit( 16.0 );
// 0 01111111100 0000000000000000000000000000000000000000000000000000
// 0 01111111101 0000000000000000000000000000000000000000000000000000
// 0 01111111110 0000000000000000000000000000000000000000000000000000
// 0 01111111111 0000000000000000000000000000000000000000000000000000
// 0 10000000000 0000000000000000000000000000000000000000000000000000
// 0 10000000001 0000000000000000000000000000000000000000000000000000
// 0 10000000010 0000000000000000000000000000000000000000000000000000
// 0 10000000011 0000000000000000000000000000000000000000000000000000
// 指数のビットは、整数とほぼ同じです。
// ただし、2の-1023乗の時に00000000000、
// 2の1023乗の時に11111111111となります。
// 残りのビットには仮数部が格納されます。
outputDoubleBit( 4.0 );
outputDoubleBit( 4.5 );
outputDoubleBit( 5.0 );
outputDoubleBit( 5.5 );
outputDoubleBit( 6.0 );
outputDoubleBit( 6.5 );
outputDoubleBit( 7.0 );
outputDoubleBit( 7.5 );
outputDoubleBit( 8.0 );
// 0 10000000001 0000000000000000000000000000000000000000000000000000
// 0 10000000001 0010000000000000000000000000000000000000000000000000
// 0 10000000001 0100000000000000000000000000000000000000000000000000
// 0 10000000001 0110000000000000000000000000000000000000000000000000
// 0 10000000001 1000000000000000000000000000000000000000000000000000
// 0 10000000001 1010000000000000000000000000000000000000000000000000
// 0 10000000001 1100000000000000000000000000000000000000000000000000
// 0 10000000001 1110000000000000000000000000000000000000000000000000
// 0 10000000010 0000000000000000000000000000000000000000000000000000
// 仮数部は、左から0.5、0.25、0.125を意味します。
// この仮数部を足した値+1を指数部に掛けたものが結果になります。
// 仮数部は「2の分数」なので、指数部の間の数(この例だと4~8の間の数)
// 全てを表現することはできません。
// そのため、「4.1」なんていうごく普通の値すら正確には表現できません。
outputDoubleBit( 4.1 );
// 0 10000000001 0000011001100110011001100110011001100110011001100110
// この値は「4.1の近似値」であり、正確には「4.1」ではありません。
// たとえば、4.1 + 8.2を計算すると、12.3になりません。
String format = "0.00000000000000000000000000000000000000000000000000";
DecimalFormat decimalFormat = new DecimalFormat( format );
System.out.println( decimalFormat.format( 4.1 + 8.2 ) );
// 12.29999999999999900000000000000000000000000000000000
// このように、浮動小数点は「正確な値を表現する」目的には使用できません。
// BigDecimalクラスを使用するようにしましょう。
}
/**
* double型変数をビット形式で出力します。
*/
private static void outputDoubleBit( double d )
{
// double型変数をビット形式で文字列化します。
String source = Long.toBinaryString( Double.doubleToLongBits( d ) );
// 左0埋めします。
StringBuffer strbuf = new StringBuffer();
for( int iF1 = source.length(); iF1 < 64; ++iF1 )
{
strbuf.append( "0" );
}
strbuf.append( source );
// 符号、仮数部、指数部の間にスペースを入れます。
strbuf.insert( 12, " " );
strbuf.insert( 1, " " );
System.out.println( strbuf.toString() );
}
}






